5 Bayesian analysis
Bayesian search was conducted in MrBayes v3.2.6 (Ronquist et al. 2012) using the Mk model (Lewis 2001) with a gamma parameter:
lset coding=variable rates=gamma;
Branch length was drawn from a dirichlet prior distribution, which is less informative than an exponential model (Rannala et al. 2012), but requires a prior mean tree length within about two orders of magnitude of the true value (Zhang et al. 2012). To satisfy this latter criterion, we specified the prior mean tree length to be equal to the length of the most parsimonious tree under equal weights, usinga Dirichlet prior with \(α_T = 1\), \(β_T = 1/\)(equal weights tree length / number of characters), \(α = c = 1\):
prset brlenspr = unconstrained: gammadir(1, 0.33, 1, 1);
Neomorphic and transformational characters (sensu Sereno 2007) were allocated to two separate partitions whose proportion of invariant characters and gamma shape parameters were allowed to vary independently:
charset Neomorphic = 2 3 5 10 13 14 18 19 24 25 29 30 32 34 36 37 38 39 40 43 50 51 53 54 55 60 63 64 67 70 72 73 76 77 78 79 84 88 89 92 94 95;
charset Transformational = 1 4 6 7 8 9 11 12 15 16 17 20 21 22 23 26 27 28 31 33 35 41 42 44 45 46 47 48 49 52 56 57 58 59 61 62 65 66 68 69 71 74 75 80 81 82 83 85 86 87 90 91 93;
partition chartype = 2: Neomorphic, Transformational;
set partition = chartype;
unlink shape=(all) pinvar=(all);
Neomorphic characters were not assumed to have a symmetrical transition rate – that is, the probability of the absent → present transition was allowed to differ from that of the present → absent transition, being drawn from a uniform prior:
prset applyto=(1) symdirihyperpr=fixed(1.0);
Four MrBayes runs were executed, each sampling eight chains for 1 000 000 generations, with samples taken every 500 generations:
mcmcp ngen=1000000 samplefreq=500 nruns=2 nchains=8;
The first 10% of samples were discarded as burn-in (burninfrac=0.1), and a posterior tree topology was derived from the combined posterior sample of both runs.
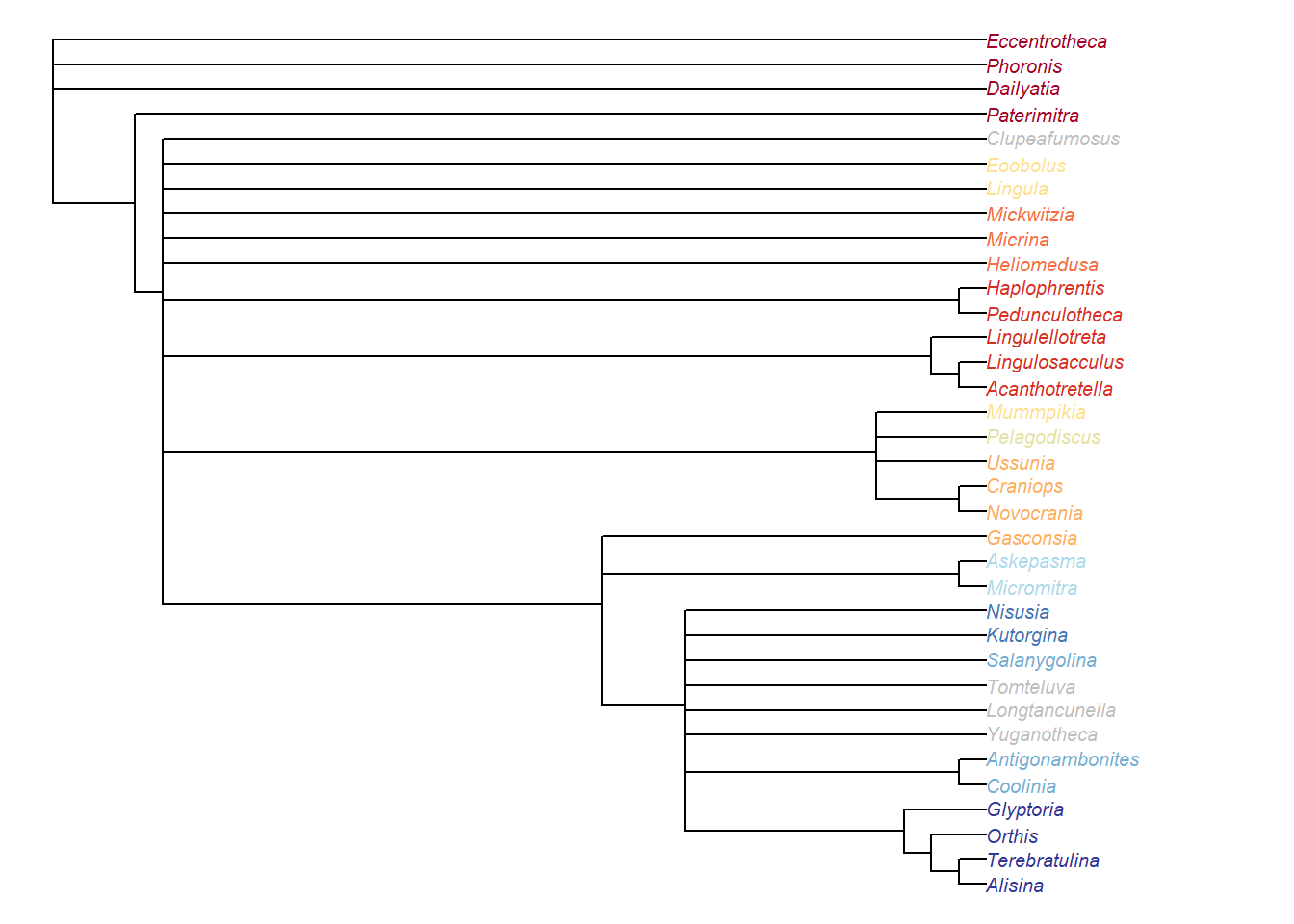
Figure 5.1: Bayesian analysis, posterior probability > 50%
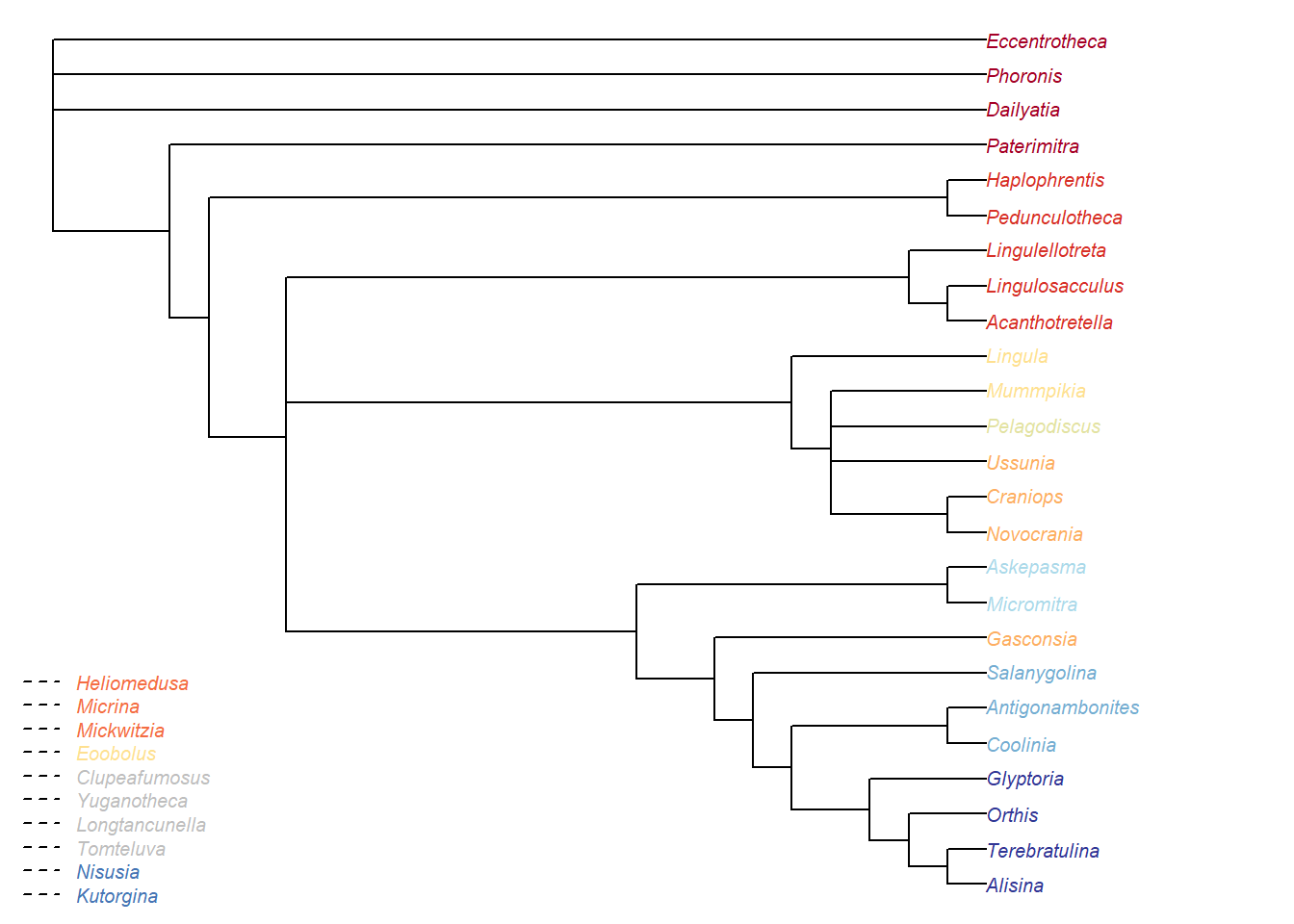
Figure 5.2: Bayesian analysis, posterior probability > 50%
Convergence was indicated by PSRF = 1.00 and an average estimated sample size of > 500 for each parameter:
| Parameter | Mean | Variance | Lower | Upper | Median | minESS | avgESS | PSRF |
|---|---|---|---|---|---|---|---|---|
| TL{all} | 6.708892 | 1.624940 | 4.8329690 | 9.249889 | 6.781895 | 9.742945 | 877.9326 | 1.022541 |
| alpha{1} | 2.403829 | 1.536554 | 0.0001827 | 4.702963 | 2.194241 | 23.533840 | 1038.9600 | 1.005475 |
| alpha{2} | 2.950148 | 2.036612 | 0.0022876 | 5.567708 | 2.770201 | 22.238850 | 1073.5860 | 1.004902 |
It’s interesting to note that the clade of hyoliths + lingulellotretids (+ relatives) is resolved as a grade under Bayesian analysis.
In parsimony analysis, these taxa are always resolved as a clade when inapplicable data is correctly handled; they instead resolve as a grade under certain conditions under the standard Fitch algorithm (which mishandles inapplicable data).
We suggest that the failure of Bayesian analysis to recover this group as a clade may reflect inappropriate handling of inapplicable data in MrBayes, though at present (and until the algorithms used in a likelihood context are improved) it is difficult to test this hypothesis.
The same goes for the position of Gasconsia, which is widely held to have an affinity with the craniid brachiopods, and is recovered in such a position using the inapplicable-safe parsimony algorithm (but not always when the standard Fitch parsimony algorithm is used).
References
Ronquist, F., M. Teslenko, P. van der Mark, D. L. Ayres, A. Darling, S. Hohna, B. Larget, L. Liu, M. A. Suchard, and J. P. Huelsenbeck. 2012: MrBayes 3.2: Efficient Bayesian phylogenetic inference and model choice across a large model space. Systematic Biology 61:539–542.
Lewis, P. O. 2001: A likelihood approach to estimating phylogeny from discrete morphological character data. Systematic Biology 50:913–925.
Rannala, B., T.-Q. Zhu, and Z.-H. Yang. 2012: Tail Paradox, Partial Identifiability, and Influential Priors in Bayesian Branch Length Inference. Molecular Biology and Evolution 29:325–335.
Zhang, C., B. Rannala, and Z.-H. Yang. 2012: Robustness of compound Dirichlet priors for Bayesian inference of branch lengths. 61:779–784.
Sereno, P. C. 2007: Logical basis for morphological characters in phylogenetics. Cladistics 23:565–587.