52. El tour del caballo¶

Un problema muy célebre en el mundo de las matemáticas es el Knight’s Tour problem. Se trata de encontrar un camino recorrido por un caballo de ajedrez desde una casilla de comienzo de manera que recorre todas las casillas del tablero de ajedrez sin pasar dos veces por ninguna.

El caballo de ajedrez se mueve trazando una L de 2x1 casillas en cualquier dirección. Por ejemplo, en la figura se muestran las ocho posibles casillas a las que puede moverse el caballo.

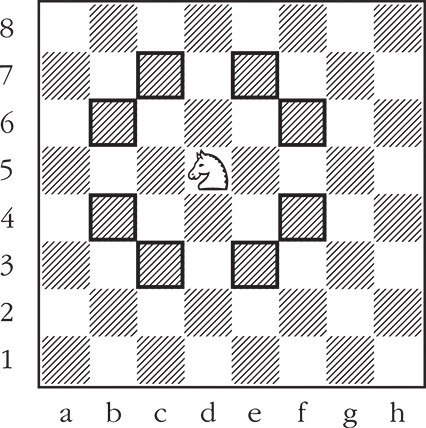
Movimientos del caballo

Pensemos ahora el problema que nos ocupa. Tenemos como entrada una posición inicial y como salida una secuencia (e.g. lista) de casillas que debe recorrer el caballo, en orden. La primera casilla de la solución es la posición inicial. En total deben aparecer todas las casillas del tablero. Es decir el resultado es una permutación de las 64 casillas del tablero.

Esto nos abre la puerta para explorar cuánto costaría resolverlo por fuerza bruta. Todas las posibles permutaciones de 64 casillas son:

import math
math.factorial(64)

126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000

Evidentemente no es planteable resolverlo por fuerza bruta. El siguiente paso es intentar una búsqueda empleando el mismo algoritmo de backtrackig que usábamos en el problema de la mochila01 cuando modelábamos el problema como un árbol de decisiones. Explorábamos la opción de coger cada elemento y no cogerlo y nos quedábamos con la mejor de las dos opciones.

La diferencia es que ahora tenemos ocho posibles casillas para decidir como destino en cada movimiento, en lugar de dos. Otra diferencia interesante es que en este problema no tenemos que explorar todo el árbol, podemos parar en cuanto encontremos una solución.

Empecemos por modelar el entorno, el tablero, los movimiento del caballo, los posibles vecinos de cada casilla.

X,Y = 8,8
casillas = [(x,y) for x in range(X) for y in range(Y)]
movimientos_caballo = [ (1,2), (1,-2), (-1,2), (-1,-2), \
                        (2,1), (-2,1), (2,-1), (-2,-1) ]
def casillas_vecinas(p):
    x,y = p
    return [ (x+dx,y+dy) for dx,dy in movimientos_caballo \
                 if x+dx in range(X) and y+dy in range(Y) ]

vecinos = { p: casillas_vecinas(p) for p in casillas }

El problema a resolver se puede plantear de forma recursiva. Tenemos una serie de movimientos que ya se han realizado y una serie de casillas ue quedan por visitar. Se trata de completar la lista de los movimientos de forma recursiva. Por ejemplo:

def caballo(inicial):
    return buscar_camino((inicial,), set(casillas) - {inicial})

def buscar_camino(movimientos, pendientes):
    if len(pendientes) == 0:
        return movimientos

    def alcanzables(x):
        return [v for v in vecinos[x] if v in pendientes]

    posibles = alcanzables(movimientos[-1])
    for siguiente in posibles:
        intento_movimientos = movimientos + (siguiente,)
        intento_pendientes = pendientes - {siguiente}
        try:
            return buscar_camino(intento_movimientos, intento_pendientes)
        except ValueError:
            pass
    raise ValueError('Sin solución')

Si ya no quedan casillas que visitar hemos terminado y el resultado es la lista de movimientos. Si no tendremos que determinar qué casillas son alcanzables desde la última posición del caballo. Para que sea una opción válida debe ser una casilla alcanzable con el movimiento del caballo pero también tiene que ser una casilla no visitada (debe estar en el conjunto de casillas pendientes).

Podríamos haber usado listas para todo, pero a veces compensa pensar cuál es la mejor estructura de datos para este caso. Por ejemplo, en la lista de casillas pendientes debe comprobarse continuamente si cada posible casilla destino está o no. La operación de pertenencia in está especialmente optimizada en los conjuntos. Sin embargo los movimientos necesitan mantener el orden, por lo que una lista o tupla es lo apropiado. Uso tuplas porque no son mutables, y de esta forma me aseguro de que no meto la pata alterando el valor del argumento.

El programa está hecho pero si intentamos ejecutarlo veremos que no encuentra el resultado. Tarda muchísimo. Es muy fácil acelerarlo si orientamos la exploracion del espacio de búsqueda hacia las opciones más probables.

Un heurístico muy efectivo es el debido a Wandorf. Dice que la exploración debe realizarse primero hacia las casillas desde las que se puede saltar a menos casillas. Es decir, hacia las casillas que más limitan la movilidad. El razonamiento es sencillo. Si dejamos estas casillas para el final será muy difícil salir de ellas, nos quedaremos atrapados. Las modificaciones son mínimas.

def caballo(inicial):
    return buscar_camino((inicial,), set(casillas) - {inicial})

def buscar_camino(movimientos, pendientes):
    if len(pendientes) == 0:
        return movimientos

    def alcanzables(x):
        return [v for v in vecinos[x] if v in pendientes]

    def wandorf(x):
        return len(alcanzables(x))

    posibles = sorted(alcanzables(movimientos[-1]), key=wandorf)
    for siguiente in posibles:
        intento_movimientos = movimientos + (siguiente,)
        intento_pendientes = pendientes - {siguiente}
        try:
            return buscar_camino(intento_movimientos, intento_pendientes)
        except ValueError:
            pass
    raise ValueError('Sin solución')

caballo((0,0))

((0, 0),
 (1, 2),
 (2, 0),
 (0, 1),
 (1, 3),
 (0, 5),
 (1, 7),
 (3, 6),
 (5, 7),
 (7, 6),
 (6, 4),
 (7, 2),
 (6, 0),
 (4, 1),
 (6, 2),
 (7, 0),
 (5, 1),
 (3, 0),
 (1, 1),
 (0, 3),
 (1, 5),
 (0, 7),
 (2, 6),
 (4, 7),
 (6, 6),
 (7, 4),
 (5, 5),
 (6, 7),
 (7, 5),
 (6, 3),
 (7, 1),
 (5, 0),
 (3, 1),
 (1, 0),
 (2, 2),
 (4, 3),
 (2, 4),
 (3, 2),
 (4, 0),
 (5, 2),
 (7, 3),
 (6, 1),
 (5, 3),
 (4, 5),
 (3, 7),
 (1, 6),
 (0, 4),
 (2, 5),
 (0, 6),
 (2, 7),
 (4, 6),
 (3, 4),
 (4, 2),
 (5, 4),
 (3, 3),
 (2, 1),
 (0, 2),
 (1, 4),
 (3, 5),
 (2, 3),
 (4, 4),
 (5, 6),
 (7, 7),
 (6, 5))

El único cambio que hemos hecho es que las opciones las ordenamos según el criterio de Wandorf. El efecto es, como ves, impresionante. De no poder encontrar una solución hemos pasado a encontrarla en décimas de segundo.