Introduction

In the previous chapter we have seen different approaches on how to work with data structures:

• Ephemeral data structures can be modified any time. Operations on data structures may or may not destroy their input.
• Persistent data structures can not be modified. Each operations creats a copy of the input with the operation applied to the output.

In this post, we build on persistent data structures and add mutation to them in a well-formed manner. Instead of blindly destroying memory cells, we keep track of computations and their dependencies in order to finally adapt dependent computation according to the modifications occured to the input. This approach is often called incremental computation in the CS literature.

A bit of History / Related Work

Incremental computation as characterized by [Ramalingam and Reps 1993] can be defined as such:

• Given some input data x and the computation result f(x), find the necessary changes of f(x) given some changes in x. Crucially here, computing the changes in the result should have incremental performance, i.e. should run in O(delta), where delta is the size of the change applied to x.

One of the first areas where incremental computation was thoroughly examined were language-based editors that need to continuously analyze the edited source-code, without disrupting the programmers work flow by performing the analysis from scratch even after only small changes [Reps et al. 1983].

Based on the idea of computing results incrementally (i.e. in running time proportional to the change), various dynamic algorithms have been developed in the algorithmics community. The field basically worked in two directions. Firstly, algorithms people took standard algorithms, derived incremental ones and showed them to be efficient. Secondly, researchers tried to develop algorithms to propagate changes in arbitrary computation graphs. By the way, this (second one) is kind of the approach we took in our first dependency paper [Worister et al. 2013]. On main problem with the general approach was how to represent changes of the dependency graph itself. Can the algorithm be used to incrementally evaluate the incremental evaluation algorithm? An extensive survey on this topic can be found in [Ramalingam and Reps 1993].

In the early 2000s, the language community started to investigate the problem of incremental computation again. In their seminal paper, [Acar et al. 2003] introduced adaptive functional programming, a technique to automatically propagate changes in purely functional programs. Later, in his thesis [Acar 2005] Acar refined adaptive funtional programming (from then called self-adjusting-computation) and showed the approach to be (provable) efficient for most programs (you can find precise definitions of most programs in his thesis).

Syntax and Semantics of our incremental language (Mod system as we call it)

An interactive Tour

This tutorial is written in literate FSharp, so in order to make it work, let us set up some infrastructure.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 

#r @"..\Packages\Aardvark.Base\lib\net45\Aardvark.Base.dll"
#r @"..\Packages\Aardvark.Base.FSharp\lib\net45\Aardvark.Base.TypeProviders.dll"
#r @"..\Packages\Aardvark.Base.FSharp\lib\net45\Aardvark.Base.FSharp.dll"
#r @"..\Packages\Aardvark.Base.Essentials\lib\net45\Aardvark.Base.Essentials.dll"
#r @"..\Packages\Aardvark.Base.Incremental\lib\net45\Aardvark.Base.Incremental.dll"
#r @"..\Packages\Aardvark.Base.Incremental\lib\net45\Aardvark.Base.Incremental.dll"
#r @"..\Packages\FAKE\tools\FakeLib.dll"

open System
open Aardvark.Base
open Aardvark.Base.Incremental

The Mod Module

Aardvark.Base.Incremental provides two essential types: IMod and ModRef<'a>

The associated operations live in the Mod module which somewhat looks like:

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 

module Mod' =

    (* mod constructors *)

    // creates a mod cell which can be changed afterwards (data source)
    let init       (v : 'a) : ModRef<'a> = ``...some implementation...``()
    // creates a mod cell which cannot be changed by the user
    let constant   (v : 'a) : IMod<'a>   = ``...some implementation...``()

    (* mod combinators *)

    // maps over a mod and creates a new one (tracks dependency)
    let map (f : 'a -> 'b) (m : IMod<'a>) : IMod<'b> = ``...some implementation...``()
    // value dependent map over mod cell (tracks dependency, dependency graph is dynamic)
    let bind (f : 'a -> IMod<'b>) (m : IMod<'a>) : IMod<'b> = ``...some implementation...``()
    // maps over two mods and runs f on the consistent inputs.
    let map2 (f : 'a -> 'b -> 'c) (m : IMod<'a>) (m' : IMod<'b>) : IMod<'c> = ``...some implementation...``()

    (* meta operations *)
    
    // changes the content of a ModRef. Only valid within transact function (see below)
    let change (r : ModRef<'a>) (newValue : 'a) : unit = ``...some implementation...``()

    // scope for supplying changes to the system. in f there might be calls to change (defined above).
    // after transact, all dependencies know that they are inconsistent and need to be recomputed on demand
    let transact (f : unit -> 'a) : 'a = ``...some implementation...``()

    // makes the content of a modifiable observable to the user
    let force (m : IMod<'a>) : 'a = ``...some implementation...``()

Let us now define the semantics for each of the operations step-by-step:

1: 

let constantMod = Mod.constant 10

Mod.constant creats a new modifiable cell which is not modifiable (funny hmm?). The purpose of this operator is to create values, which can be fed to the system (so that it typechecks), although the thing is not really modifiable. Nevertheless, the operation creates a new cell with initially no outputs.

1: 

let modRef1 = Mod.init 10

Mod.init creats a new modifiable cell which can be changed afterwards:

1: 

let mappedref = Mod.map (fun s -> s + 1) modRef1

Mod.map creats a fresh modifiable cell, adds the dependency to its single source and taggs conceptually tags the introduced edge with the function supplied as first argument.

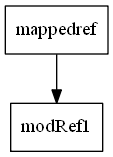
Whenever its source is changed, f needs to be reexecuted in order to make the result consistent again.

1: 

Mod.force mappedref |> printfn "mappedRef=%d"

prints 11, since modRef1 has value 10 and map increments its value

1: 
2: 
3: 

transact (fun () ->
    Mod.change modRef1 0
)

performs a modification on the input cell, which due to the semantics of transact results in marking mappedRef to be invalid. *

1: 

Mod.force mappedref |> printfn "mappedRef=%d"

prints 1, since the input value modref1 was changed to have value 0, and due to transact mappedref was marked to be inconsisted. Mod.force is guaranteed to always return the consistent value of the supplied mod. Thus, Mod.force carries all operations, required to make mappedref consistent again, reads out the constitent value which is finally handled over to printfn.

So far, our dependency graphs are entirely static, i.e. each operation adds an edge to exactly one source node. In order to formulate arbitrary functional programs it is necessary to express dynamic dependencies. More precisely, depending on the actual avalue of an IMod<'a> we would like to proceed in different sub dependency graphs. To be honest, this is the core of our system and buzzled us for a long time.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 

let dynamicDependency // implements value level dependency
     (m : IMod<'a>)   // source mod which we depend on per value
     (cont : 'a -> #IMod<'b>) // A continuation function. Whenever ``m``'s value changes,
                              // we call ``cont`` which in turn returns us a complete 
                              // dependency graph. (ignore the # for the moment)
     : IMod<'b> = ``...some implementation...``()

let g1 = Mod.init 10 
let g2 = Mod.init 20
let s = Mod.init true
let g3 = dynamicDependency s (fun s -> if s then g1 else g2)

Wow, the code type-checks. So of course we must have found the right primitve... right? Incident?? Not really. ... Let us recall LINQ which essentially provides a module (removing C# clutter and wrong return type placement):

1: 
2: 
3: 

module IEnumerable =
    let select (xs : seq<'a>) (f : 'a -> 'b) : seq<'b> = ``...some implementation...``()
    let selectMany (xs : seq<'a>) (f : 'a -> seq<'b>) : seq<'b> = ``...some implementation...``()

Ok... what we got here in select is just map (trivial by seq ~ IMod). Let us now look at selectMany. selectMany applies a seqence creation function per element of an input sequence and flattens the result. In mod world, in dynamicDependency we apply a continuation function to the actual value of the mod and return a inner mod which is returned to the outer level. Again, by substituting seq ~ IMod we can convert between the prented functions. Turns out that this goes back to the mathematican [Moggi 1991] and [Wadler 1995] who firstly used monads in the context of programming. Later this monad stuff was used in LINQ [Meijer et al. 2006],[Syme 2006] and many many many others. In order to respekt zollen we from now on call dynamicDependency bind. Let us now get back to dependencies and how to use bind in practise.

So far we can create input boxes and boxes depending on another single box. This is rather useless, right?. Let us now implement a more complex dependency graph.

1: 
2: 
3: 
4: 
5: 

let mode = Mod.init true
let inputA = Mod.init 5
let inputB = Mod.init 10
let multiplyInputs = Mod.map2 (fun a b -> a * b) inputA inputB
let addInputs = Mod.map2 (fun a b -> a + b) inputA inputB

1: 
2: 
3: 

// here comes the shit. Bind extracts the value of a mod thingy and dependent on
// its value it returns different mods, i.e. different dependency grpahs.
let output = Mod.bind (fun m -> if m then multiplyInputs else addInputs) mode

Since mode is true, we return the multiplyInputs graph. As you can see the complete addInputs graph is not even existent:

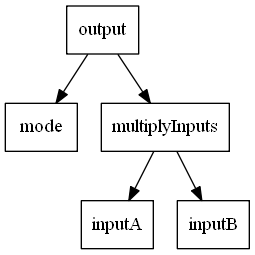
1: 
2: 
3: 
4: 
5: 
6: 

// change the mode
transact (fun () -> Mod.change mode false)

// compute the result of output

output |> Mod.force |> printfn "output is: %d"

Since mode is now true, we return the addInputs graph. As you can see the complete multipleInputs graph is not even existent:

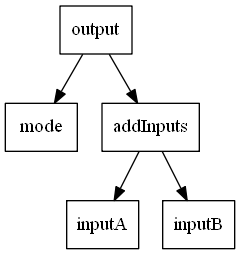
Of course working with those boring combinators can be painful when working with complex graphs. Luckily, in F# we can do better by creating a computation expression builder which internally, calls our primitives, i.e. creates a dependency graph under the hood. Given the inputs introduced earlier we can use this syntactic sugar in order to retrieve much nicer code:

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

let output2 = 
    adaptive {
        let! m = mode
        if m then
            return! multiplyInputs
        else 
            return! addInputs
    }

output2 semantically behaves exactly like output, which can be seen by inspecting the dependency graph

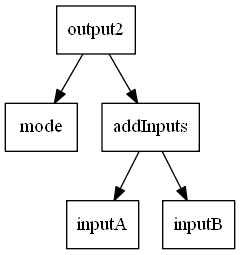
Semantically, let! behaves like let, but introduces a dependency edge.

Correct usage of the operators introduced so far

Our implementation is very kind to the user (at first). Almost everything compiles, but there are some things which need to be taken care of when writing adaptive code (i.e. we check some static properties at runtime instead of compile time for pragmantic reasons... ammmm or something we check nothing and you get garbagge!!).

• Mod.change can only be used in transact. We enforce this at runtime.
• transact and change shall never occur in an adaptive lambda function like the one handed over to map. Repeat after me. No transact in stuff which is reexecuted by the mod system.
• Although it might be useful to use Mod.force in adaptive functions it at least smells bad. Mod.force extracts the value of an IMod without adding an edge to the dependency graph.

1: 
2: 
3: 
4: 
5: 
6: 
7: 

let a =
    adaptive {
        let! m = Mod.init 10
        let! c = Mod.init 20
        let! d = Mod.init 30
        return m + c + d
    } 

Academic background of our implementation

Our approach is inspired by [Acar et al. 2003] and [Acar 2005]. The computation expression builder (aka monad) is (a tiny bit if you want) similar to the one presented by [Carlsson 2002]. However the semantics is unpublished, yet somewhat inspired by [Hudson et al. 1991]: eager marking, lazy evaluation. Notably, in parallel to our efforts, [Hammer et al. 2014] published our change propagation sheme.