• theory & terminology
• introductory example
• objective
• usage
  • automatic optimization
  • live examples
• implementation
  • regular type
  • equivalence in detail
  • notes
• advanced class design for value semantics

what is a value?

what we can already see:

• equality is less restrictive than identity
  → identical objects are always equal
  → equal objects are not necessarily identical
• equality does not necessarily depend on an objects underlying physical representation
  → e.g. equality can be defined between instances of
       different types
• things are quite simple when dealing with unique values
  → e.g. numbers, strings, dates

what do we actually want here?

→ modify v by scaling each of it's elements by some factor x

• of cause we don't want to modify a local copy, so we get v by reference and modify whatever instance it refers to
• but what is the reason for getting x by reference? probably someone intended to suppress a spare copy?

is it even correct to get x by reference? NO!

scale(v, v[0])

passing x by reference introduced a hidden dependency,
causing a side-effect in our example

in general with using references we are referring to remote objects,
making the code more complicated, because it prohibits local reasoning

that's where we go much easier with values!

⇓

void scale(std::vector &v, double x)
{
  for (size_t i = 0; i != v.size(); ++i)
    v[i] /= x;
}

why leveraging value semantics?

• it results in simpler code, because we don't need to manage object identity
  → improve locality
  → avoid unnecessary dependencies
• going towards saying what we want instead of specifying how it is done
  → makes it easier for others to understand our code
• it faciliates regular types
  → better code reuse
  → same syntax for the same semantics

why do we so often tend to use references,
even if semantically there is no need to?

because references were always known
to be more efficient

→ c++ devs are used to optimize their code manually
→ sometimes on the cost of code simplicity

the interesting point is:

• with using a reference we declared identity, where we only needed equivalence!

• for the compiler this means our declaration is more restrictive! it has less freedom to optimize

with value semantics we get better code
and take advantage of automatic optimization

"tell the compiler that you are interested in values rather than objects, and the compiler chooses the best tool to implement your intentions"
^{(Andrzej Krzemieński)}

as-if rule: [...] an implementation is free to disregard any requirement of this International Standard as long as the result is as if the requirement had been obeyed, as far as can be determined from the observable behavior of the program.
^{(§1.9.1, ISO C++11 Standard)}

→ in general the compiler can perform arbitrary optimizations as long as it results in the same behavior

copy elision: When certain criteria are met, an implementation is allowed to omit the copy/move construction of a class object, even if the copy/move constructor and/or destructor for the object have side effects.
^{(§12.8.31, ISO C++11 Standard)}

→ copies and moves are made “in principle”, the compiler is allowed to optimize them away

→ regarding the as-if rule, copy/move have predefined semantics

copy/move construction should only be implemented explicitly for:

• RAII classes to encapsulate resources
• implementing optimizations

otherwise the compiler generated ones should be just fine (they simply copy all members on copy and move all members on move)

to be discussed design-wise: prefer rule of zero, rule of five defaults or
defaulted c/d-tors with assign by value?

but!

• make sure your type supports value semantics!
  → make first steps with std types

things are easy as long as we deal with unique values
(like arithmetic values, dates, etc.)

e.g. we have a lot of different representations of the decimal integer 5:

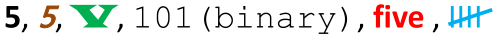
• the value itself is a logical entity
• it's independent of which physical representation is used
• think of a c++ object as just another representation!

• equality-comparable
• default-constructible
• assignable (⇒ copyable and/or movable)

in general a type's public interface should ensure this:

if (a == b)
{
  op1(a); op1(b); assert(a == b);
  op2(a); op2(b); assert(a == b);
  op3(a); op3(b); assert(a == b);
  op4(a); op4(b); assert(a == b);
}

in math what we talk about is called an equivalence relation:

• a == a (reflexive)
• a == b  ⇔  b == a (symmetric)
• a == b && b == c  ⇒  a == c (transitive)

obviously operator== must define an equivalence relation

symmetry ⇒ it's best to define operator== free-standing!
^{for a more technical explanation see: John Lakos, "Value Semantics" (2014), p. 193 ff}

given two std::vector's differing only in their capacity()

are they equivalent?

..let's have a look at some simpler examples first..

class rational_t {
public:
  int numerator() const;
  int denominator() const;

private:
  ...
};

bool operator==(const rational_t &lhs, const rational_t &rhs)
{
  < implementation? >
}

salient attributes?    →    ??

class rational_t {
public:
  int num() const;
  int denom() const;

private:
  ...
};

bool operator==(const rational_t &lhs, const rational_t &rhs)
{
  long long ext_fraction1 = (long long)lhs.num() * rhs.denom();
  long long ext_fraction2 = (long long)rhs.num() * lhs.denom();

  return ext_fraction1 == ext_fraction2;
}

→ asking for salient attributes can be misleading

→   std::vector::capacity() is there for technical reasons only:

• a modified vector could have its capacity always set to its size
• it would just reallocate on every push and pop, but this is an implementation detail
• its observable behavior could not be distinguished from the original vector

→   std::vector::capacity() is an optimization:

• optimizations may be used to overcome drawbacks that arise from certain physical representations
• optimizations must not affect an objects logical state
• an objects logical state must not depend on optimizations

in other words: when a and b are vectors with different capacities,
we still expect the same behavior!

if (a == b)
{
  op1(a); op1(b); assert(a == b);
  op2(a); op2(b); assert(a == b);
  op3(a); op3(b); assert(a == b);
  op4(a); op4(b); assert(a == b);
}

there is one issue when working with values all the time..

we don't have polymorphism!
because that requires aliases which requires referenceness

as a solution for this, Sean Parent proposes:
"polymorphism as an implementation detail"

• Shifing polymorphism from type to use allows for greater reuse and fewer dependencies
• Using regular semantics for the common basis operations, copy, assignment, and move helps to reduce shared objects
• Regular types promote interoperability of sofware components, increases productivity as well as quality, security, and performance
• There is no necessary performance penalty to using regular semantics, and ofen times there are performance benefts from a decreased use of the heap