The electric field phasor of a plane wave propagating in the $+z$ direction is \begin{aligned} \vec{E} &= \vec{E}_0 \mathrm{e}^{-jkz}\\ &= \left(\hat{x}E_{x0} + \hat{y}E_{y0}\right)\mathrm{e}^{-jkz} \end{aligned} where $E_{x0}$ and $E_{y0}$ are in general complex, i.e., \begin{aligned} E_{x0} &= |E_{x0}|\mathrm{e}^{j\delta_x} \\ E_{y0} &= |E_{y0}|\mathrm{e}^{j\delta_y} \end{aligned} such that \begin{aligned} \vec{E} &= \left(\hat{x}|E_{x0}|\mathrm{e}^{j\delta_x} + \hat{y}|E_{y0}|\mathrm{e}^{j\delta_y}\right)\mathrm{e}^{-jkz}\\ &= |E_{x0}|\mathrm{e}^{j\delta_x}\left(\hat{x} + \hat{y}\frac{|E_{y0}|}{|E_{x0}|}\mathrm{e}^{j(\delta_y-\delta_x)}\right)\mathrm{e}^{-jkz}\\ &= |E_{x0}|\mathrm{e}^{j\delta_x}\left(\hat{x} + \hat{y}\tan\psi\,\mathrm{e}^{j\delta}\right)\mathrm{e}^{-jkz},\\ \end{aligned} where \begin{aligned} \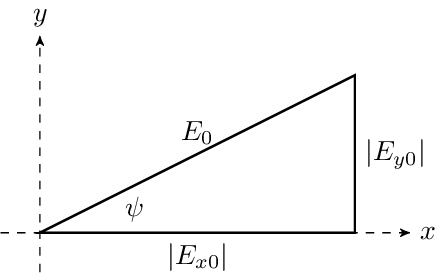tan\psi &= \frac{|E_{y0}|}{|E_{x0}|} \text{ (ratio of the amplitude of the y-component to the x-component)} \\ \delta &= \delta_y-\delta_x \text{ (phase of the y-component relative to the x-component)} \end{aligned} with \begin{aligned} 0 \le \psi \le \pi \\ -\pi \lt \delta \le \pi. \end{aligned} The angle, $\psi$, can be understood graphically as

where the amplitude of the phasor (and therefore the real electric field) is $E_0 = |\vec{E}| = \sqrt{|E_{x0}|^2 + |E_{y0}|^2}$. Note from the figure that \begin{aligned} |E_{x0}| &= E_0 \cos{\psi} \\ |E_{y0}| &= E_0 \sin{\psi}. \\ \end{aligned} The real electric field is \begin{aligned} \vec{\mathcal{E}}(z,t) &= \operatorname{Re}(\vec{E}\, \mathrm{e}^{j\omega t}) \\ &= \hat{x}|E_{x0}|\cos(\omega t - kz + \delta_x) + \hat{y}|E_{x0}|\tan\psi\cos(\omega t - kz + \delta_x + \delta)\\ &= E_{0}\left[\hat{x}\cos{\psi}\cos(\omega t - kz + \delta_x) + \hat{y}\sin{\psi}\cos(\omega t - kz + \delta_x + \delta)\right], \\ \end{aligned} where $\operatorname{Re}()$ means take the real part. For ease of visualization, consider the electric field in the $z=0$ plane with $\delta_x = 0$, in which case the real electric field is \begin{aligned} \vec{\mathcal{E}}(0,t) &= E_{0}\left[\hat{x}\cos{\psi}\cos(\omega t) + \hat{y}\sin{\psi}\cos(\omega t + \delta)\right]. \\ \end{aligned} The visualization below shows the path traced by the electric field vector (blue curve) in the $z=0$ plane as a function of $\psi$ and $\delta$. When the animation is started, the instantaneous electric field vector is shown as a red arrow.

Start Reset

Special Cases

• Linear Polarization: $\psi = 0^{\circ} \text{ or } 90^{\circ}$, OR $\delta = 0^{\circ} \text{ or } 180^{\circ}$
• Circular Polarization: $\psi = 45^{\circ}$ AND $\delta = \pm90^{\circ}$