12th May 2016

Bayesian time series analysis

We can start by thinking of time series analysis as a regression problem, with

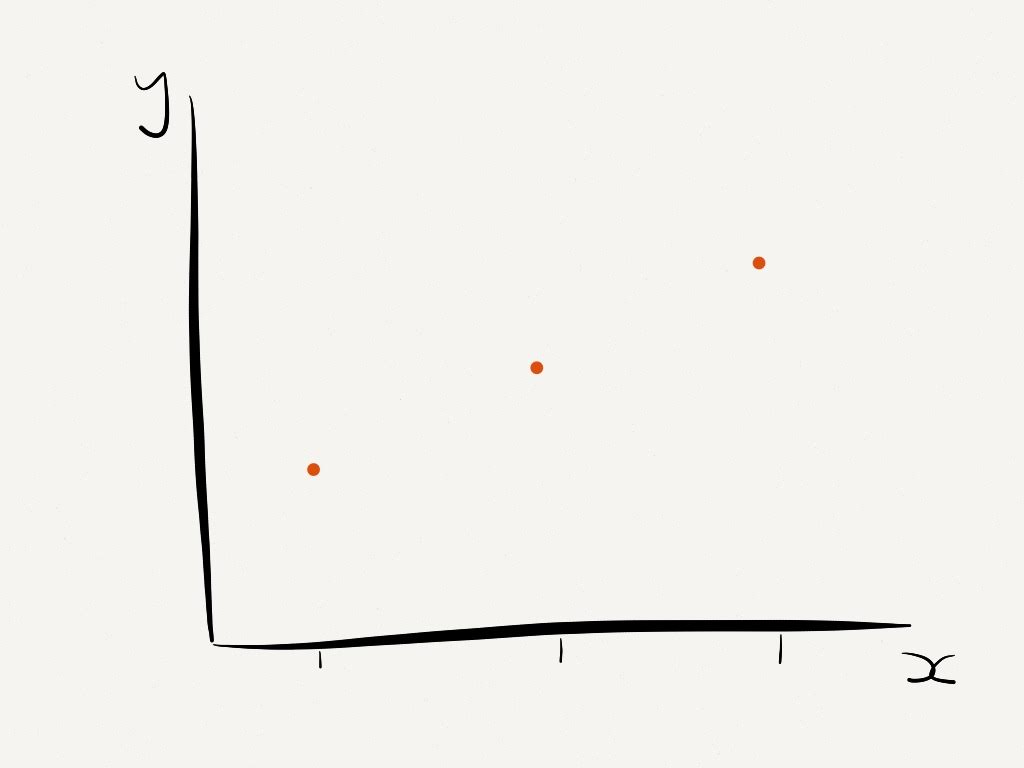
\[ y(x) = f(x) + \epsilon\]

Where \(y(x)\) is the output of interest, \(f(x)\) is some function and \(\epsilon\) is an additive white noise process.

We would like to:

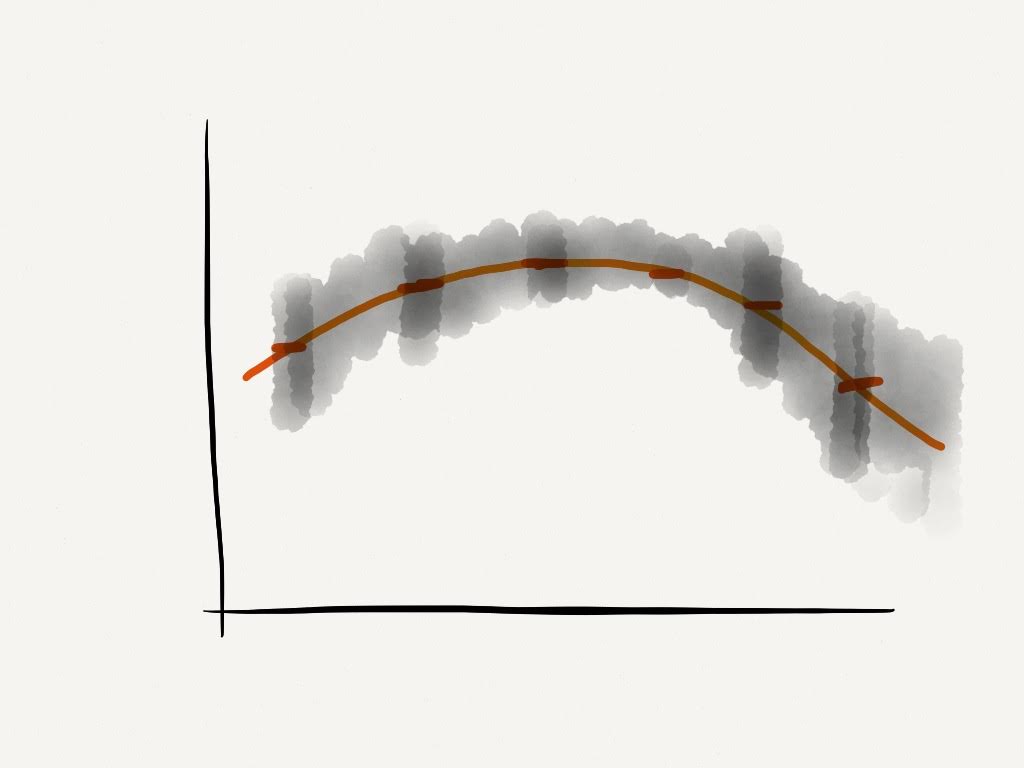
  1. Evaluate \(f(x)\)
  2. Find the probability distribution of \(y^*\) for some \(x^*\)

We make the assumption that \(y\) is ordered by \(x\), we fit a curve to the points and extrapolate.

Bayesian time series analysis

Bayesian time series analysis

Bayesian time series analysis

But! Bayes' theorem naturally encodes Occam's razor:

"Among competing hypotheses, the one with the fewest assumptions should be selected."

The solutions with tighter curves are more complex and contain more assumptions.

Bayesian time series analysis

What is a Gaussian process?

The multivariate Normal distribution for GPs

  • Start with a 2-dimensional normal distribution, with the shape defined by a 2x2 covariance matrix.

The multivariate Normal distribution for GPs

The multivariate Normal distribution for GPs

  • An observation on one dimension changes distribution of the other (and reduces uncertainty).
  • The conditional distribution \(p(x_{2}|x_{1}=x)\) is different from the marginal.

The multivariate Normal distribution for GPs

Extend to a two-observation time series

An observation on \(x_1\) changes the conditional ditribution for \(x_2\)

Or for a longer time series

We can extend to continuous time

The covariance function

The GP relies on the covariance kernel function, which has the general form \(k(x_{1}, x_{2})\)

We might choose something like

\[k(x_{1}, x_{2}) = \tau^2 exp[- \rho(x_{1}-x_{2})^2]\]

So that the covariance reduces as the distance between \(x_1\) and \(x_2\) increases, depending on length parameter \(\rho\).

The maths

\(y\) is the vector of observations of \(y_t\), a response variable at time \(t\). We can model \(y\) as drawn from a multivariate Normal distribution:

\[ y \sim MVN(\mu, \Sigma)\] \(\mu\) is some mean function and \(\Sigma\) is a covariance matrix where \[\Sigma_{ij} = k(x_{1}, x_{2}) = \tau^2 e^{-\rho(t_{i} - t_{j})^{2}}\] if \(i \neq j\)

The covariance matrix

Choices of covariance function

  • The choice of covaraiance function encodes our prior knowledge about the process - smoothness, stationarity, periodicity.
  • We can build up a covariance function by parts, for example adding a linear or sinusoidal part.
  • There is some good guidance on choosing correlation functions in the MUCM toolkit

The nugget term

  • The diagonal \((i=j)\) of the covariance matrix contains the information about the uncertainty relationship between a point and itself!

  • If there is NO uncertainty at a point, the mean function is constrained to go through the point (this is useful for deterministic computer models).

  • We can add a nugget, so that the mean function isn't constrained.

if \(i \neq j\) \[\Sigma_{ij} = \tau^2 +\sigma^2\] if \(i=j\) (i.e. on the diagonal).

The nugget term

Advantages of using GPs

  • Freer in form than some models
  • Highly flexible, general and can apply to many problems
  • Can get some very good predictions
  • Lets the data "speak for itself"

An example in regression

Disadvantages of using GPs

  • Can be dependent on good priors
  • Can be more difficlut to interpret parameters to understand the underlying model
  • Slow for large data sets (including in JAGS)

Fitting GPs in JAGS

Notation

# y(t): Response variable at time t, defined on continuous time
# y: vector of all observations
# alpha: Overall mean parameter
# sigma: residual standard deviation parameter (sometimes known in the GP world as the nugget)
# rho: decay parameter for the GP autocorrelation function
# tau: GP standard deviation parameter

Sampling from A GP

# Likelihood:
# y ~ MVN(Mu, Sigma)
# where MVN is the multivariate normal distribution and
# Mu[t] = alpha
# Sigma is a covariance matrix with:
# Sigma_{ij} = tau^2 * exp( -rho * (t_i - t_j)^2 ) if i != j
# Sigma_{ij} = tau^2 + sigma^2 if i=j
# The part exp( -rho * (t_i - t_j)^2 ) is known as the autocorrelation function

# Prior
# alpha ~ N(0,100)
# sigma ~ U(0,10)
# tau ~ U(0,10)
# rho ~ U(0.1, 5) # Need something reasonably informative here

Simulate from the GP

T = 20 # default is 20 can take to e.g T = 100 but fitting gets really slow ...
alpha = 0 # default is 0
sigma = 0.03 # default is 0.03
tau = 1 # default is 1
rho = 1# default is 1
set.seed(123) # ensure reproducablility
t = sort(runif(T))
Sigma = sigma^2 * diag(T) + tau^2 * exp( - rho * outer(t,t,'-')^2 )
y = mvrnorm(1,rep(alpha,T), Sigma)

Simulate from the GP

Fit a GP model to the data using JAGS

# Jags code to fit the model to the simulated data
model_code = '
model
{
  # Likelihood
  y ~ dmnorm(Mu, Sigma.inv)
  Sigma.inv <- inverse(Sigma)
  
  # Set up mean and covariance matrix
  for(i in 1:T) {
    Mu[i] <- alpha
    Sigma[i,i] <- pow(sigma, 2) + pow(tau, 2)
  
    for(j in (i+1):T) {
      Sigma[i,j] <- pow(tau, 2) * exp( - rho * pow(t[i] - t[j], 2) )
      Sigma[j,i] <- Sigma[i,j]
    }
  }
  
  alpha ~ dnorm(0, 0.01) # default dnorm(0, 0.01)
  sigma ~ dunif(0, 10) # default dunif(0,10)
  tau ~ dunif(0, 10) # default dunif(0, 10)
  rho ~ dunif(0.1, 5) # default dunif(0.1, 5)
  
} 
'
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 1
##    Unobserved stochastic nodes: 4
##    Total graph size: 1411
## 
## Initializing model

Make predictions using the GP

Resources