In this lecture we will:

• Learn some key time series concepts and features
• Get to see some of the example time series that we'll use on the course
• Understand the types of analysis that we want to do, and why
• Learn to avoid some common mistakes

• A collection of data indexed by (strictly increasing) time
• Can be regular or irregular
• Usually one value per time

“With one dimension marching along to the regular rhythm of seconds, minutes, hours, days, weeks, months, years, centuries, or millennia, the natural ordering of the time scale gives this design a strength and efficiency of interpretation found in no other graphic arrangement.”

Edward R. TufteThe Visual Display of Quantitative Informationp. 28

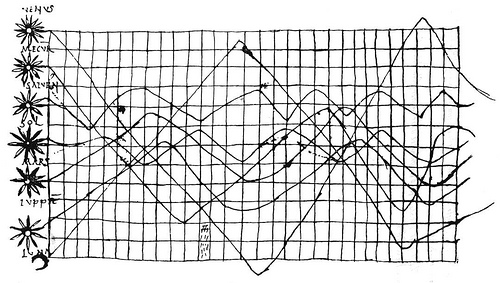
Tenth or eleventh century time series showing the position of the planets with time.http://euclid.psych.yorku.ca/SCS/Gallery/milestone/sec2.html

Diagram showing the distance of the planets to the earth in 1732, also showing a complete lunar eclipse and a partial solar eclipse in that yearNicolaas Kruik 1678 - 1754 Dutch Astronomer & Meteorologist

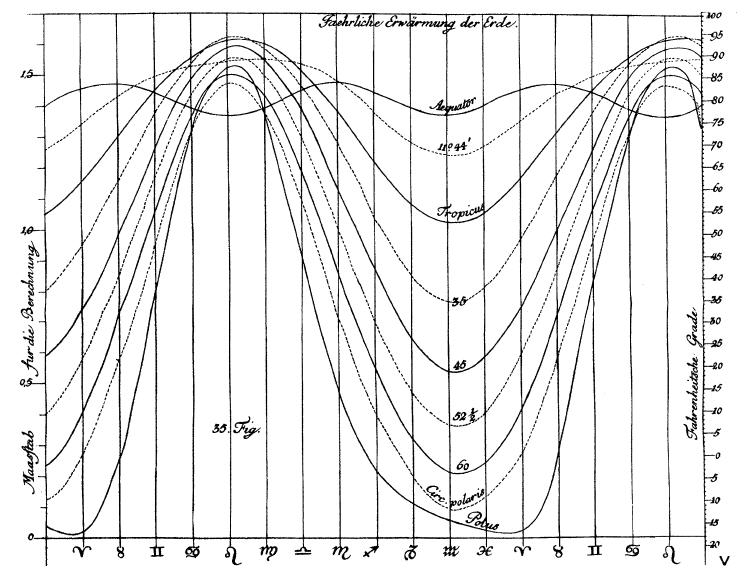
A graph of solar warming vs. lattitude.
Johann Heinrich Lambert 1728 - 1777

Willaim Playfair's trade-balance time-series chart, published in his Commercial and Political Atlas, 1786

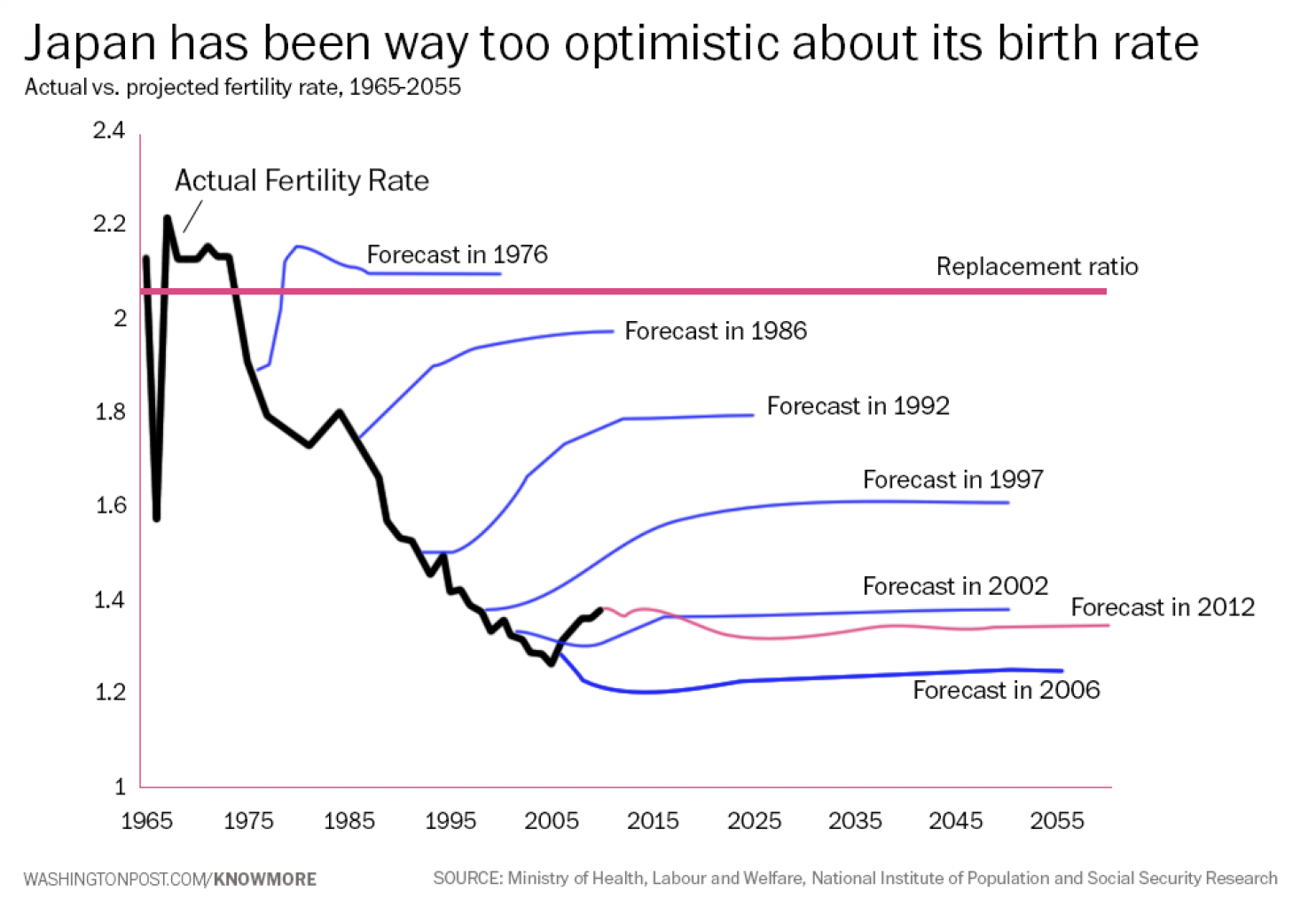
What do we use time series methods for? Often, we are trying to do at least one of the following:

1. Description: what is going on?
2. Understanding: how is it going on, and why?
3. Prediction: What is going to go on next?

• Using a line plot gives a slightly different impression.

So, what is structure?

And what is random?

And, how does that randomness manifest?

• Church and White
• There appears relatively less noise in this data compared to the trend

We know there is randomness and uncertainty in the time series. We can use a statistical model to help us understand and predict the system. This usually proceeds:

1. Model identification and selection
2. Parameter estimation
3. Model checking

There are a number of features of time series and concepts that help in the process …

• Time series may show periodicity and cycles - often seasonal, but perhaps with more complexity.

plot(ldeaths)

• This AirPassengers data set shows heteroskedasticity - changes in variability.

plot(AirPassengers)

• This data shows heteroskedacity and regime changes and a lot of structure

• Autocorrelation is the correlation of a random process with itself at a different time.

• When we smooth a time series, we are applying a filter to try and remove some of the randomness, and get at (or remove) the underlying structure.
• We are making assumptions, and imposing structure. You have to put something in in order to get something out.

• In a stationary time series mean, variance and autocorrelation structure do not change over time.
• Stationarity is a common assumption in some types of time series analysis.

• A time series of the differences between the values.
• Differencing can be used used to make a non-stationary trend stationary.
• First differencing removes a linear trend, \(k\)th-order differencing removes a polynomial trend of order \(k\)

This is the lynx data set, annual numbers of lynx trappings for Canada 1821 - 1934. Regarded as representative of the population.

plot(lynx)

• Reilly and Zeringue (2004) use a simple dynamic predator-prey model, trained on the first 80 years of data, to predict the last 34.
• The simple model outperforms many of the best time series methods.
• RMS error of 1480, compared to 1600 for SETAR method fit with entire data set.http://andrewgelman.com/2012/01/28/the-last-word-on-the-canadian-lynx-series/

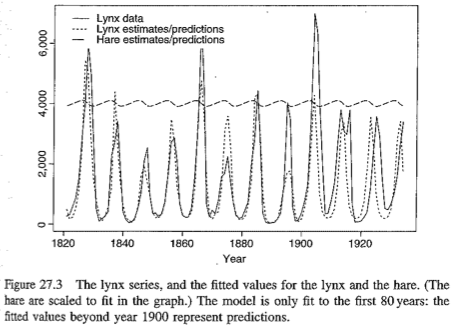
(Graphic from D. Spiegelhalter)

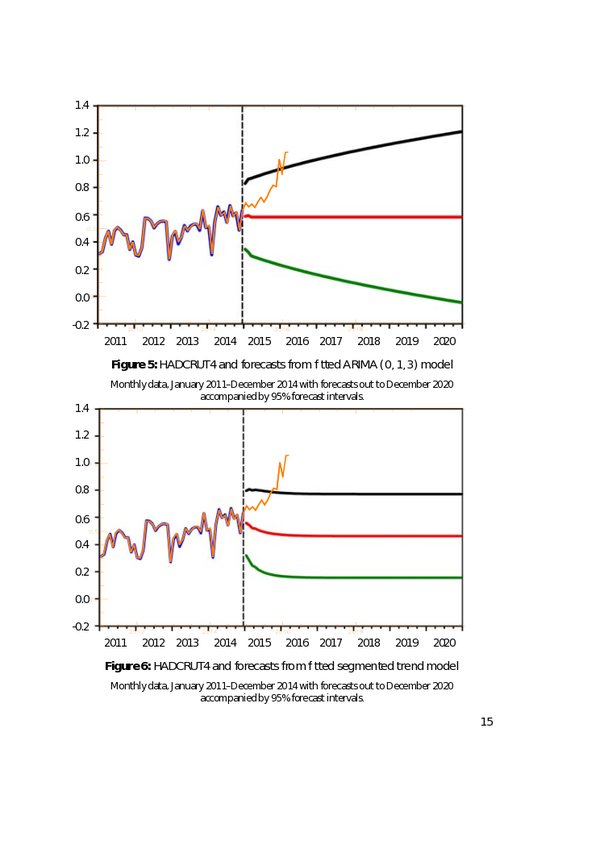
This course takes a practical approach, and should help you:

• Understand modern Bayesian modelling techniques.
• Get and use tools for thinking about and dealing with uncertainty.
• Fit time series models, and make predictions.
• Understand your time series data, and the process that generates it.